La comparaison de modèles est un levier puissant pour analyser les phénomènes que l'on cherche à représenter, et les restituer au mieux en fonction des critères à optimiser. Cette notion inclut la comparaison des modalités d'implémentation d'algorithmes. D'ailleurs l'incapacité à comparer des modèles, pour des raisons variées, témoigne souvent d'un manque de reproductibilité des travaux, et donc finalement de la qualité limitée des résultats obtenus.
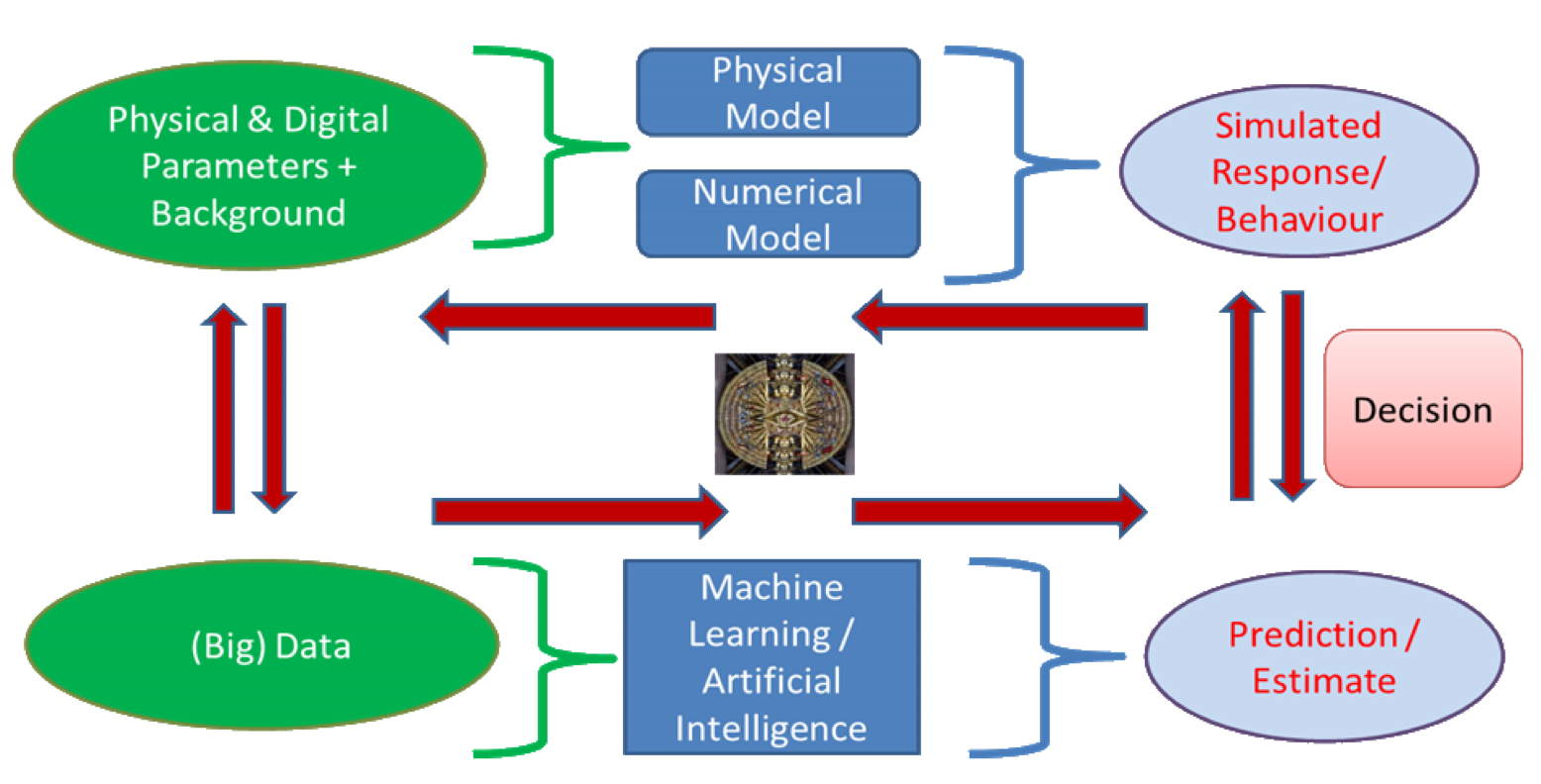
Au delà de la seule comparaison, la combinaison de modèles, ou de méthodes, peut créer des effet de synergie. Ainsi en est-il de la combinaison de modélisations respectivement cyberphysiques et statistiques. Une telle combinaison permet de disposer d'une représentation d'ensemble permettant des décisions elles-mêmes optimisées.
Alors que la modélisation cyberphysique ne peut pas être résolue seule, le modèle statistique vient préciser ou qualifier des paramètres physiques. Et symétriquement, alors que les données ne sont pas , au moins initialement , suffisantes pour obtenir un apprentissage performant, le modèle cyberphysique vient pallier ce manque. Chaque approche renforce l'autre et donc l'ensemble.
